Reducing quantum compute costs 2,500X with Fire Opal


The challenge
Quantum computing resources are scarce and incredibly costly today given the lifecycle of the industry. Premium device systems are often prohibitively expensive for R&D purposes where rapid iteration and prototyping can easily accumulate millions of dollars in compute expenses.
Impact
>2,500X
Reduction of quantum compute cost
The outcome
With Fire Opal, a financial company was able to run algorithms on more cost-effective hardware systems while achieving results comparable to more premium systems. By increasing the likelihood of achieving successful outcomes and reducing the total number of executions required to find useful solutions, costs were further reduced.
Companies across industries and sectors are turning to quantum computing as a potential means to solve problems that are currently out of reach for classical computers. Optimization problems are universal across industries, and research has demonstrated that there is a possibility that quantum computing can provide meaningful speedup with regard to many problems that cannot be efficiently solved by classical computers today.
Organizations such as Transport for New South Wales, have turned to Q-CTRL to find solutions to challenges such as optimization of logistics routing, scheduling, and planning.
Beyond transportation, finance is another sector with major potential for disruption via quantum computing since many valuable problems in the industry are computationally hard. Of these problems, portfolio optimization is one of particular interest for many financial institutions.
Financial organizations are currently piloting the development of quantum applications which early adopters will put to their own strategic advantage. In search of a fiscally sustainable and scalable way to validate and apply methods of portfolio optimization on quantum computers, one financial institution (who for now shall remain nameless) turned to Fire Opal to secure more insight from their budget.
Fire Opal helped lower costs in three major ways:
- Enabling the institution to use more cost-effective hardware through the simple addition of performance-management software, which delivered performance comparable to more expensive devices
- Reducing the total number of executions required for each optimization cycle, by improving the process of algorithmic “convergence”
- Improving the overall probability of finding the correct answer and thereby reducing the total number of experiments required
Cost concerns are a commonly cited pain point across financial services institutions developing quantum-computing use cases like portfolio optimization. Both researching and applying these methods is compute- and cost-intensive, particularly since the costs of quantum compute resources are far more expensive than their classical counterparts. Moreover, optimization problems require repeated executions and high device quality, which typically means using much more compute time on the most expensive hardware.
In this “land-grab” era of use-case development, financial organizations want to iterate rapidly and test a broad range of options as they develop proprietary capabilities—here cost efficiency is critical.
Portfolio optimization on quantum computers
One of the most valuable financial applications amenable to quantum solutions is portfolio optimization. This broadly refers to the process of selecting a range of assets and asset classes according to some objective. Typically the objective is to maximize or minimize a target; for example, maximizing future return or minimizing risk. The problem space is especially challenging due to external constraints that can be placed on the objective, such as the need for diversification or compliance with regulations.1
Classical approaches to portfolio optimization are limited by complex algorithms whose resources grow rapidly with the problem size. That’s why this company’s research team is evaluating algorithms like the Quantum Approximate Optimization Algorithm (QAOA) to solve these sorts of problems.
QAOA can be used to solve the relevant optimization problems by formulating the goal, whether it's return maximization or risk minimization, as a cost function. The cost function is then encoded as a quantum Hamiltonian—a mathematical representation of the energy of a quantum system. The algorithm finds the best solution by executing a small quantum algorithm in an iterative loop of classical optimization until an answer is found that meets the goal.
Estimating compute time and costs of QAOA
Because QAOA is a variational quantum algorithm, it is inherently more expensive to run than deterministic algorithms. Each experiment requires tens or hundreds of quantum circuit executions due to the back-and-forth between the quantum and classical parts of the algorithm.
On top of that, this particular company found that they were only able to achieve any sort of results with a single hardware provider because other providers’ devices were too susceptible to error. The team was apprehensive since the hardware provider would be significantly more expensive than others evaluated. They performed an analysis given their implementation of QAOA and how much it would cost to perform experiments with that provider.
Their implementation of QAOA was designed to solve an experimental constrained optimization problem. The technique to impose the constraints relies on the use of multiple mid-circuit measurements during the circuit. The QAOA circuit’s properties vary depending on the level of approximation used and require 5 qubits, up to 160 two-qubit gates, up to 400 single-qubit gates, and up to 60 measurement/reset operations.
The research team estimated that, for convergence, they would need to conduct roughly 100 executions of the QAOA circuit with 2000 shots (repetitions needed for averaging) each. Using the hardware provider’s pay-as-you-go pricing through Azure Quantum, the estimated cost was roughly $89,205. This was only the cost of a single experiment. If the team had to run the experiment more than 10 times, they would quickly rack up $1 million in compute costs. Not to mention, putting the implementation into production would mean even greater costs.
Saving over 500X by making the most of low-cost hardware
It was important for the company’s team to find a more scalable and cost-effective hardware provider, but other devices were simply too error-prone. After spending a few weeks trying out various error mitigation strategies, the team finally came upon Fire Opal.
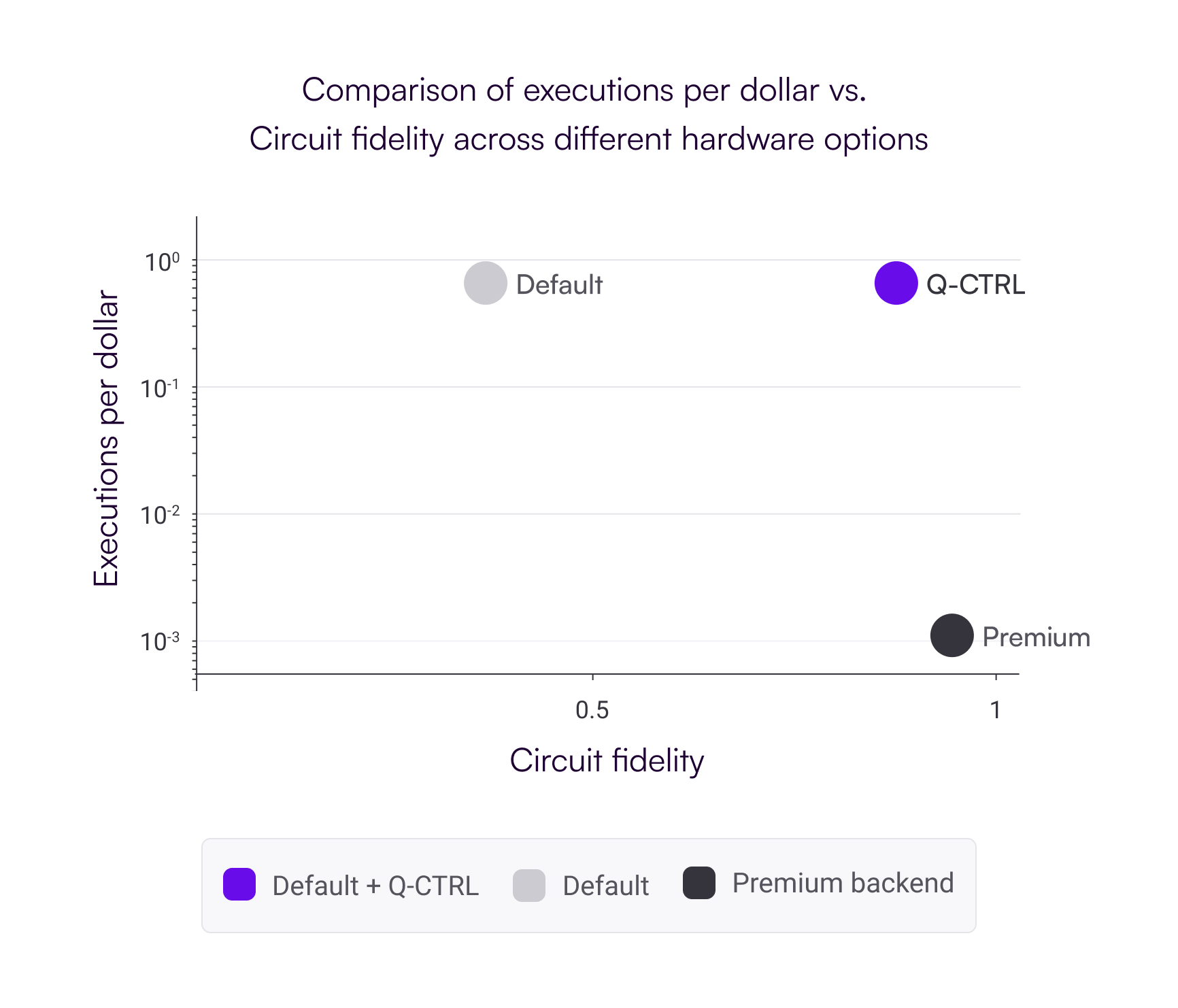
Fire Opal was the solution they needed to suppress errors on lower-cost devices. By running circuits through Fire Opal’s `.execute` function, the team was able to get meaningful results on devices that they’d previously deemed unusable. The results from the low-cost devices were now comparable to the premium hardware vendor—the performance gap was closed.
They performed the same cost estimation exercise and found that running the same QAOA loop with 100 executions and 2000 shots on the low-cost device was only $160. This meant a cost savings of 558X without a degradation in performance.
Getting to 2,500X savings with less!
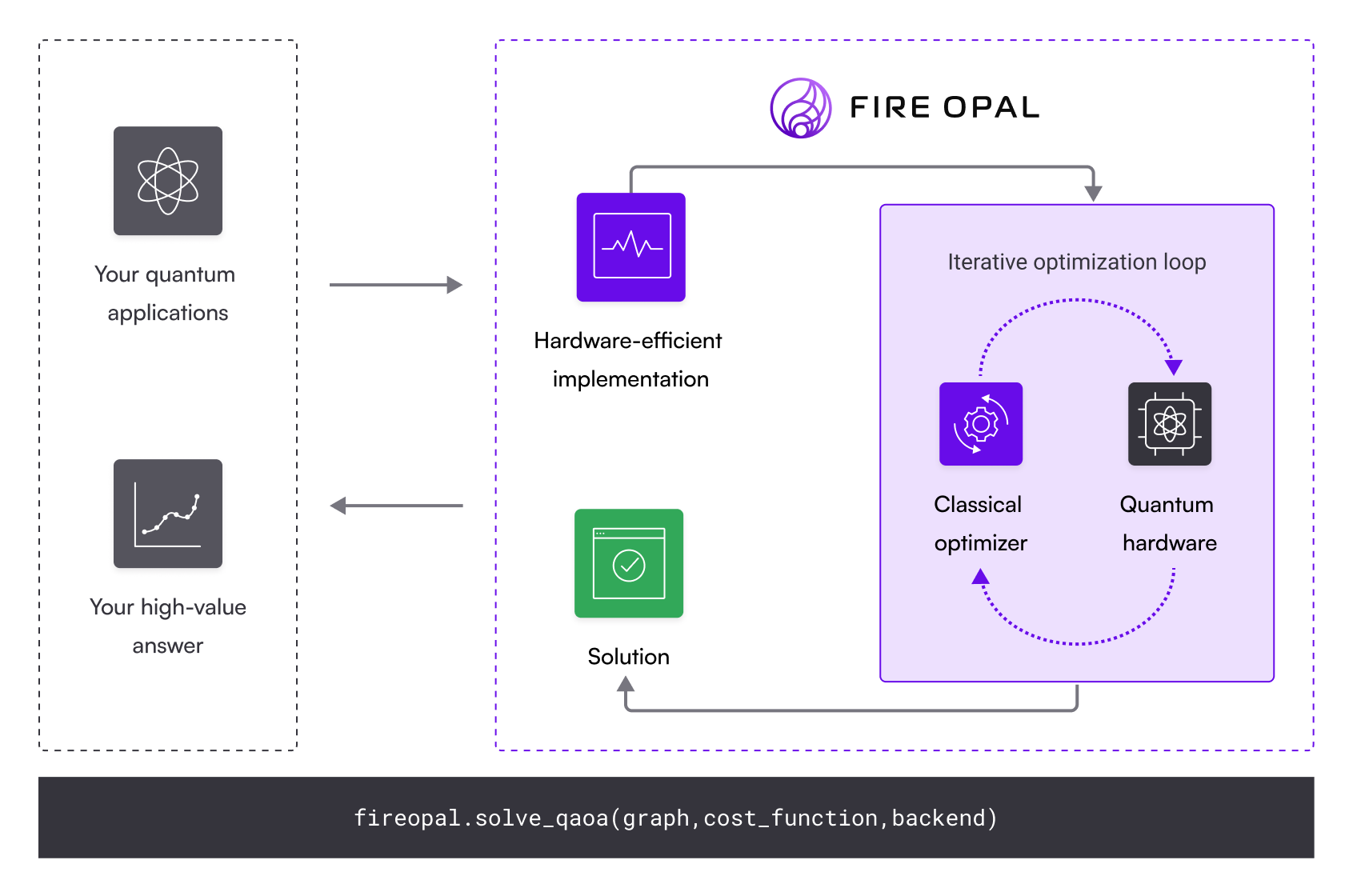
The team also tried out Fire Opal’s `.solve_qaoa` function, which packages all aspects of executing QAOA into a single command. This resulted in further improvements to cost efficiency. The solver function converged consistently within 20 or fewer executions, which allowed them to reduce the assumption of 100 executions per experiment to just 20. With the faster convergence, a single hybrid loop execution would be 5X cheaper—only $32.
On top of that, Fire Opal’s QAOA solver consistently yielded correct results, which meant that each time they had to update the objective, they would only have to rerun the algorithm once, as opposed to going through a trial-and-error process of 10 or more experiments—yielding another 10X in compute reduction.
Q-CTRL’s technology helped achieve the best possible balance of performance and cost. It achieved nearly identical performance to a high-end premium device, but for 2,500X lower compute cost!
Putting Fire Opal into practice
All in all, the customer was able to drastically lower the compute costs of their R&D cycle for portfolio optimization. The estimates went from a projected $89,205 for a single run of a QAOA algorithm to only $32, yielding a cost efficiency gain of >2,500X.
The increased cost efficiency allows the team to feel confident that they will be able to scale their development methods without having to worry about resource allocation. The team has defaulted to using Fire Opal for any testing that needs to be performed on real devices, which can be done more frequently.
To start saving on your compute costs get started with Fire Opal and use our QAOA solver for free today!








