The fingerprint of noise

When conducting a criminal investigation, discovering a fingerprint can help identify the culprit. Q-CTRL is creating tools to help manufacturers of quantum computers identify the sources of interference or noise that limit the performance of their qubits, the building blocks of quantum machines.

With this new knowledge it's possible to develop workarounds in order to minimize the impact of this noise on the quantum computer.

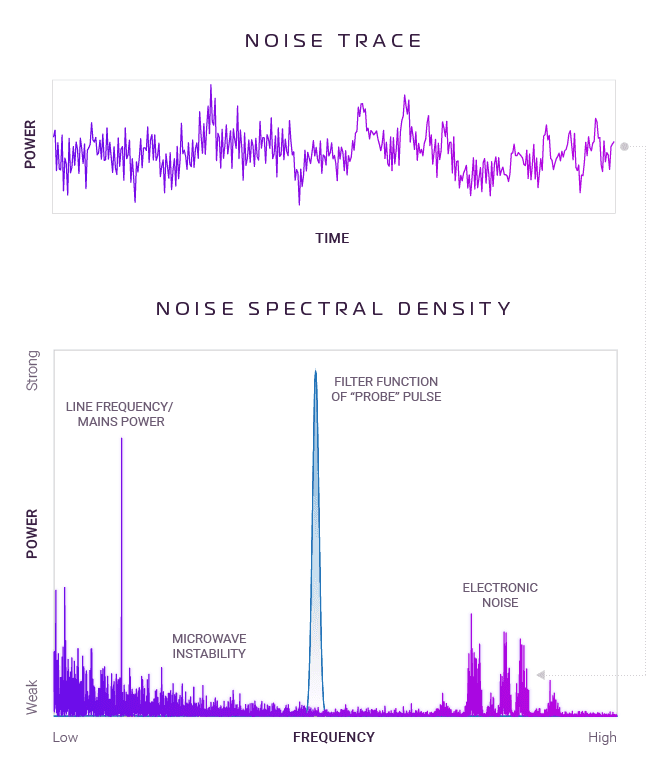
The fingerprint of noise is its "spectral density" - a measure of how strong the interference is as a function of frequency, or pitch (the lower panel in the graph below). The spectral density represents the same information as the time recording of the noise, but in a way that's more useful for our purposes. This is because different noise sources will contribute different signatures in a noise spectral density in an easily identifiable way, while most noise time traces are indistinguishable to you and me.

For example, line frequency (mains power) is modulated at 50 or 60 hertz depending on where you live, so noise from a power source can appear as a large spike at this frequency. You can see that spike in the graph below.

By mapping the spectral density of the noise affecting your quantum device you can identify what sources are creating the most significant problems for your actual physical qubits.

In classical electrical engineering a carefully calibrated noise source of a known power distribution can be used to generate a particular signal. This can then be fed through a circuit to test the amount and type of noise it is producing. The result is a spectral density distribution that tells you where your circuit is adding (unwanted) noise.

Assembling this sort of 'fingerprint' for quantum hardware is challenging because, unlike a classical circuit, once we make a measurement of the qubit we are testing we collapse its quantum state. So we only get one piece of information per computation before needing to reset and start again.

Q-CTRL has come up with a solution to the challenge of generating noise spectral density profiles for the hardware inside quantum computers. Our approach simplifies the necessary measurements as well as the subsequent data processing.

We have previously looked at how Q-CTRL can use filter functions to analyse control pulses generated by laser or microwave radiation. These filter functions let us know what frequencies a qubit will be sensitive to under application of a specific control.

Instead of just suppressing noise as we discussed last time, we can also craft control pulses that result in a filter function that is narrowly peaked around a specific frequency. That is, the controls can make the qubit "listen" to its environment only over a narrow range while excluding other signals. In the lower panel of our graph, the blue feature shows the frequency response of our probe pulse. This spike will sweep across the graph as we test for noise at different frequencies.

This approach allows the qubit itself to become a selective probe for measuring how much noise is present at a particular frequency. By adding tools to shift the sensitivity point, we can map out the noise spectral density.

Moreover, we can do this all in a way that is mathematically provable to be the best we can possibly achieve in terms of excluding other signals interfering with our measurement.

This is the power of our filter-function framework for quantum control.

Once a noise spectral density has been assembled - and particular noise sources identified from it - experimentalists can try to remove the source. If this is not possible, Q-CTRL can provide control solutions tailored to mitigate the effects of this noise on computation.

These controls might be a previously demonstrated solution, or one uniquely designed for the specific noise profiled with the spectral density via our optimization package. Ultimately, our control solutions can help teams dramatically improve the performance of their hardware.

When we return to this subject next time, we'll give you an example of how we use machine learning to derive high performing controls tailored to suppress a user's noise.

‍